JUAN ANGEL VELASQUEZ LOPEZ

Unidad 1: Interpretación de información

ELEMENTOS DE LA ESTADÍSTICA

PRINCIPALES ELEMENTOS DE LA ESTADISTICA

DESCRIPTIVA
Resume las propiedades de una poblacion y se basa en la teorio de las probabilidades.

DIFERENCIAL
Generaliza de la muestra a conjunto de datos sin inferir de la muestra a la población

CONCEPTOS GENERALES
La estadística se divide en dos grupos.

POBLACIÓN
Es el conjunto de todos los elementos a los que se somete a un estudio estadístico.

INDIVIDUO
Es cada uno de los elementos que compone la población.

MUESTRA
Es un conjunto representativo de la población de referencia, el número de individuos de una muestra es menor que el de la población.

MUESTREO
Es la reunión de datos que se dese estudiar, obtenidos de una proporción reducida y representativa de la población.

VALOR
Es cada uno de los distintos resultados que se pueden obtener en un estudio estadístico.

VARIABLES
Cualitativas
Cuantitativas
No pueden ser medidas con números.

CUALI. ORDINAL
Se expresa mediante números, se puede realizar operaciones.

DISTRIBUCIÓN DE FRECUENCIAS

En estadística, se le llama distribución de frecuencias a la agrupación de datos en categorías mutuamente incluye que indican el número de observaciones en cada categoría. 

FRECUENCIA COMPLETA

La frecuencia completa por su denominación es el número de veces que aparece un determinado valor en un valor estadístico. Se representa por fila. La suma de la frecuencia completa es igual al número total de datos, que se representa por N. Para indicar resumidamente estas sumas se utiliza la letra griega Σ (sigma mayúscula) que se lee sumatoria. 

FRECUENCIA RELATIVA

Se dice que la frecuencia relativa es el cociente entre la frecuencia absoluta de un determinado valor y el número total de datos. Se puede expresar en tantos por ciento y se representa por h_i. La suma de las frecuencias relativas es igual a 1.

Frecuencia relativa (h_i) es el cociente entre la frecuencia absoluta y el tamaño de la muestra (N). Es decir:

siendo el fi para todo el conjunto i. Se presenta en una tabla o nube de puntos en una distribución de frecuencias.

Si multiplicamos la frecuencia relativa por 100 obtendremos el porcentaje o tanto por ciento (pi).

FRECUENCIA ACUMULADA

La frecuencia acumulada es la suma de las frecuencias absolutas de todos los valores inferiores o iguales al valor considerado.

La frecuencia acumulada es la frecuencia estadística F(XXr) con que el valor de un variable aleatoria (X) es menor que o igual a un valor de referencia (Xr).

La frecuencia acumulada relativa se deja escribir como Fc(X≤Xr), o en breveFc(Xr), y se calcula de:

Fc  = Hxr / N

donde MXr es el número de datos X con un valor menor que o igual a Xr, y N es número total de los datos. En breve se escribe:

Fc  = M  /  N

Cuando Xr=Xmin, donde Xmin es el valor mínimo observado, se ve que Fc=1/N, porque M=1. Por otro lado, cuando Xr=Xmax, donde Xmax es el valor máximo observado, se ve que Fc=1, porque M=N.

En porcentaje la ecuación es

Fc (%)  = 100  M  /  N

DISTRIBUCIÓN DE FRECUENCIAS AGRUPADAS

La distribución de frecuencias agrupadas o tabla con datos agrupados se emplea si las variables toman un número grande de valores o la variable es continua. Se agrupan los valores en intervalos que tengan la misma amplitud denominados clases. A cada clase se le asigna su frecuencia correspondiente. Límites de la clase. Cada clase está delimitada por el límite inferior de la clase y el límite superior de la clase.

La amplitud de la clase es la diferencia entre el límite superior e inferior de la clase. La marca de clase es el punto medio de cada intervalo y es el valor que representa a todo el intervalo para el cálculo de algunos parámetros. En caso de que el primer intervalo sea de la forma (-∞,k], o bien [k,+∞) donde k es un número cualquiera, en el caso de (-∞,k], para calcular la marca de clase se tomará la amplitud del intervalo adyacente a el (ai+1), y la marca de clase será ((k-ai+1) +k)/2. En el caso del intervalo [k,+∞) también se tomará la amplitud del intervalo adyacente a el (ai-1) siendo la marca de clase ((k+ai-1)+k)/2.

Construcción de una tabla de datos agrupados:

3, 15, 24, 28, 33, 35, 38, 42, 43, 38, 36, 34, 29, 25, 17, 7, 34, 36, 39, 44, 31, 26, 20, 11, 13, 22, 27, 47, 39, 37, 34, 32, 35, 28, 38, 41, 48, 15, 32, 13.

1. Se localizan los valores menor y mayor de la distribución. En este caso son 3 y 48.

1. Se restan y se busca un número entero un poco mayor que la diferencia y que sea divisible por el número de intervalos que queramos establecer.

Es conveniente que el número de intervalos oscile entre 6 y 15.

En este caso, 48 - 3 = 45, incrementamos el número hasta 50 : 5 = 10 intervalos.

Se forman los intervalos teniendo presente que el límite inferior de una clase pertenece al intervalo, pero el límite superior no pertenece al intervalo, se cuenta en el siguiente intervalo.

Intervalo	ci	ni	Ni	fi	Fi
[0, 5)	2.5	1	1	0.025	0.025
[5, 10)	7.5	1	2	0.025	0.050
[10, 15)	12.5	3	5	0.075	0.125
[15, 20)	17.5	3	8	0.075	0.200
[20, 25)	22.5	3	11	0.075	0.275
[25, 30)	27.5	6	17	0.150	0.425
[30, 35)	32.5	7	24	0.175	0.600
[35, 40)	37.5	10	34	0.250	0.850
[40, 45)	42.5	4	38	0.100	0.950
[45, 50)	47.5	2	40	0.050	1
Total:		40		1

MEDIA ARITMÉTICA

En matemáticas y estadística, la media aritmética, también llamada promedio o media, de un conjunto finito de números es el valor característico de una serie de datos cuantitativos, objeto de estudio que parte del principio de la esperanza matemática o valor esperado, se obtiene a partir de la suma de todos sus valores dividida entre el número de sumandos. Cuando el conjunto es una muestra aleatoria recibe el nombre de media muestral siendo uno de los principales estadísticos muestrales.

Dados los n números  , la media aritmética se define como:

$$
{\displaystyle \{x_{1},x_{2},\ldots ,x_{n}\}}

Por ejemplo, la media aritmética de 8, 5 y -1 es igual a:

Se utiliza la letra X con una barra horizontal sobre el símbolo para representar la media de una muestra (${\displaystyle {\overline {X}}}$), mientras que la letra µ (mu) se usa para la media aritmética de una población, es decir, el valor esperado de una variable.

En otras palabras, es la suma de n valores de la variable y luego dividido por n, donde n es el número de sumandos, o en el caso de estadística el número de datos se da el resultado.

MEDIANA

La mediana de un conjunto de datos es el valor que cumple que la mitad de valores están por encima y la otra mitad por debajo. Así pues, para encontrarla basta con ordenar los elementos de menor a mayor y escoger el valor central.

Cálculo de la mediana mediante el uso de tablas

Cuando se dispone de muchos datos es mucho más cómodo utilizar tablas para el cálculo de la mediana.

La mediana de un conjunto de números es el número medio en el conjunto (después que los números han sido arreglados del menor al mayor) -- o, si hay un número par de datos, la mediana es el promedio de los dos números medios.

EJEMPLO 1

Encuentre la mediana del conjunto {2, 5, 8, 11, 16, 21, 30}.

Hay 7 números en el conjunto, y estos están acomodados en orden ascendente. El número medio (el cuarto en la lista) es 11. Así, la mediana es 11.

EJEMPLO 2

Encuentre la mediana del conjunto {3, 10, 36, 255, 79, 24, 5, 8}.

Primero, arregle los números en orden ascendente.

{3, 5, 8, 10, 24, 36, 79, 255}

Hay 8 números en el conjunto -- un número par. Así, encuentre el promedio de los dos números medios, 10 y 24.

(10 + 24)/2 = 34/2 = 17

Así, la mediana es 17.

MODA

La moda se conoce como el dígito o individuo que más se repite.

En estadística, la moda es el valor con mayor frecuencia en una distribución de datos.

Se hablará de una distribución bimodal de los datos adquiridos en una columna cuando encontremos dos modas, es decir, dos datos que tengan la misma frecuencia absoluta máxima. Una distribución trimodal de los datos es en la que encontramos tres modas. En el caso de la distribución uniforme discreta, cuando todos los datos tienen la misma frecuencia, se puede definir las modas como indicado, pero estos valores no tienen utilidad. Por eso algunos matemáticos califican esta distribución como «sin moda».

El intervalo modal es el de mayor frecuencia absoluta. Cuando tratamos con datos agrupados antes de definir la moda, se ha de definir el intervalo modal.

La moda, cuando los datos están agrupados, es un punto que divide al intervalo modal en dos partes de la forma p y c-p, siendo c la amplitud del intervalo, que verifiquen que:

EJEMPLO 1

Encuentre la moda del conjunto {2, 3, 5, 5, 7, 9, 9, 9, 10, 12}.

El 2, 3, 7, 10 y 12 aparecen una vez cada uno.

El 5 aparece dos veces y el 9 aparece tres veces.

Así, el 9 es la moda.

EJEMPLO 2

Encuentre la moda del conjunto {2, 5, 5, 6, 8, 8, 9, 11}.

En este caso, hay dos modas -- el 5 y el 8 ambos aparecen dos veces, mientras que los otros números solo aparecen una vez.

VARIANZA

En teoría de probabilidad, la varianza o variancia (que suele representarse como {\displaystyle \sigma ^{2}}) de una variable aleatoria es una medida de dispersión definida como la esperanza del cuadrado de la desviación de dicha variable respecto a su media.

Hay que tener en cuenta que la varianza puede verse muy influida por los valores atípicos y no se aconseja su uso cuando las distribuciones de las variables aleatorias tienen colas pesadas. En tales casos se recomienda el uso de otras medidas de dispersión más robustas.

Comienza con un conjunto de datos de la población. El término "población" hace referencia al total de datos de las observaciones relevantes. Por ejemplo, si vas a analizar la edad de los residentes del estado de NEW YORK, tu población debe incluir la edad de cada uno de los residentes de NEW YORK. Normalmente, para un conjunto de datos tan grande como ese, crearías una hoja de cálculo. Sin embargo, aquí tienes un conjunto más pequeño de datos como ejemplo:

Ejemplo: en la habitación de un acuario hay exactamente 6 peceras. Las seis peceras contienen la siguiente cantidad de peces:

Anota la fórmula de la varianza de la población. Debido a que la población contiene todos los datos que necesitas, esta fórmula te dará el valor exacto de la varianza de la población. Para poder distinguirla de la varianza de una muestra (que es solo un valor aproximado), los estadísticos usan otras variables:

·         σ{\displaystyle ^{2}} = ^{(∑({\displaystyle x_{i}} - μ){\displaystyle ^{2}})}/_n

·         σ{\displaystyle ^{2}} = varianza de la población. Es la letra sigma minúscula, elevada al cuadrado. La varianza se mide en unidades al cuadrado.

·         {\displaystyle x_{i}} representa un término de tu conjunto de datos.

·         Los términos dentro de ∑ se calcularán para cada valor de {\displaystyle x_{i}}, y luego se sumarán.

·         μ es la media de la población.

n es la cantidad de puntos de datos de la población.

Encuentra la media de la población. Cuando analizas una población, el símbolo μ ("mu") representa la media aritmética. Para encontrar la media, suma todos los puntos de datos y luego divide el resultado por la cantidad de puntos de datos.

·         Puedes pensar en la media como el "promedio", pero ten cuidado, ya que esa palabra tiene muchas definiciones en matemática.

·         Ejemplo: media = μ = {\displaystyle {\frac {5+5+8+12+15+18}{6}}} = 10,5

Problema 1     

En la siguiente tabla se representan las cotizaciones mensuales del tipo de cambio entre el peso mexicano y el dólar estadounidense en el año 2000, este tipo de cambio se presentó en algunas casas de cambio.

Mes	Frecuencia acumulada	Frecuencia absoluta	Fracción	Decimal	Porcentaje
Enero	9.47	9.47	9.47/113.39	0.08	8%
Febrero	9.44	9.47+9.44=18.91	9.44/113.39	0.08	8%
Marzo	9.29	18.91+9.29=28.2	9.29/113.39	0.08	8%
Abril	9.37	28.2+9.37=37.57	9.37/113.39	0.08	8%
Mayo	9.50	37.57+9.50=47.07	9.50/113.39	0.08	8%
Junio	9.79	47.07+9.79=56.86	9.79/113.39	0.08	8%
Julio	9.46	56.86+9.46=66.32	9.46/113.39	0.08	8%
Agosto	9.28	66.32+9.28=75.6	9.28/113.39	0.08	8%
Septiembre	9.33	75.6+9.33=84.93	9.33/113.39	0.08	8%
Octubre	9.51	84.93+9.51=94.44	9.51/113.39	0.08	8%
Noviembre	9.51	94.44+9.51=103.95	9.51/113.39	0.08	8%
Diciembre	9.44	103.95+9.44=113.39	9.44/113.39	0.08	8%
total				9.6	96%

Las cotizaciones mensuales del tipo de cambio entre el peso y dólar	Numero de intervalo	Frecuencia absoluta	Fracción	Decimal	Porcentaje
9.28	1	1	1/12	0.083	8.3
9.29	1	1+1=2	1/12	0.083	8.3
9.33	1	2+1=3	1/12	0.083	8.3
9.37	1	3+1=4	1/12	0.083	8.3
9.44	2	4+2=6	2/12	0.166	16.6
9.46	1	6+1=7	1/12	0.083	8.3
9.47	1	7+1=8	1/12	0.083	8.3
9.50	1	8+1=9	1/12	0.083	8.3
9.51	2	9+2=11	2/12	0.166	16.6
9.79	1	11+1=12	1/12	0.083	8.3
Total	12			0.996	99.6

Problema 2

Los siguientes datos representan muestras aleatorias de edades de niños que están aprendiendo a tocar la guitarra:     9, 12, 14, 15, 13, 11, 10, 12, 11. Determina:

	Edades de niños	FI	FA	FN	FR	%F
1	15	1	1	1/9	0.11	11
2	14	1	1+1=2	1/9	0.11	11
3	13	1	2+1=3	1/9	0.11	11
4	12	2	3+2=5	2/9	0.22	22
5	11	2	5+2=7	2/9	0.22	22
6	10	1	7+1=8	1/9	0.11	11
7	9	1	8+1=9	1/9	0.11	11
	Total	9			1	100

MEDIDAS DE DISPERCIÓN

Parámetros estadísticos que indican como se alejan los datos respecto de la media aritmética. Sirven como indicador de la variabilidad de los datos. Las medidas de dispersión más utilizadas son el rango, la desviación estándar y la varianza.



RANGO

Rango el intervalo entre el valor máximo y el valor mínimo; por ello, comparte unidades con los datos. Permite obtener una idea de la dispersión de los datos, cuanto mayor es el rango, más dispersos están los datos (sin considerar la afectación de los valores extremos). Por ejemplo, para una serie de datos de carácter cuantitativo, como lo es la estatura medida en centímetros, tendríamos:

es posible ordenar los datos como sigue:

donde la notación x_(i) indica que se trata del elemento i-ésimo de la serie de datos. De este modo, el rango sería la diferencia entre el valor máximo ${\displaystyle x_{(k)}}$ y el mínimo ${\displaystyle x_{(1)}}$; o, lo que es lo mismo:

nos da que R = 185-155 = 30

En estadística la desviación absoluta promedio o, sencillamente desviación media o promedio de un conjunto de datos es la media de las desviaciones absolutas y es un resumen de la dispersión estadística.¹​ Se expresa, de acuerdo a esta fórmula:

La desviación absoluta respecto a la media, ${\displaystyle D_{m}}$, la desviación absoluta respecto a la mediana, ${\displaystyle D_{M}}$, y la desviación típica, ${\displaystyle \sigma }$, de un mismo conjunto de valores cumplen la desigualdad:

Rango es igual a:

El valor:

Unidad 2 

LEY DE LA ADICIÓN

Regla general de la adición de probabilidades para eventos no mutuamente excluyentes

Si A y B son dos eventos no mutuamente excluyentes (eventos intersecantes), es decir, de modo que ocurra A o bien B o ambos a la vez (al mismo tiempo), entonces se aplica la siguiente regla para calcular dicha probabilidad:

El espacio muestral (S) corresponde al conjunto universo en la teoría de conjuntos

Ejemplos ilustrativos

1) Sea A el suceso de sacar un As de una baraja estándar de 52 cartas y B sacar una carta con corazón rojo. Calcular la probabilidad de sacar un As o un corazón rojo o ambos en una sola extracción.

Solución:

A y B son sucesos no mutuamente excluyentes porque puede sacarse el as de corazón rojo.

Las probabilidades son:

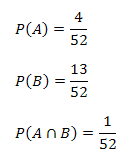
Reemplazando los anteriores valores en la regla general de la adición de probabilidades para eventos no mutuamente excluyentes se obtiene:

PROBABILIDAD CONDICIONAL

Probabilidad condicional es la probabilidad de que ocurra un evento A, sabiendo que también sucede otro evento B. La probabilidad condicional se escribe P(A|B) o P(A/B), y se lee «la probabilidad de A dado B».

No tiene por qué haber una relación causal o temporal entre A y B. A puede preceder en el tiempo a B, sucederlo o pueden ocurrir simultáneamente. A puede causar B, viceversa o pueden no tener relación causal. Las relaciones causales o temporales son nociones que no pertenecen al ámbito de la probabilidad. Pueden desempeñar un papel o no dependiendo de la interpretación que se le dé a los eventos.

Un ejemplo clásico es el lanzamiento de una moneda para luego lanzar un dado. ¿Cuál es la probabilidad que en el dado salga un 6 dado que ya haya salido una cara en la moneda? Esta probabilidad se denota de esta manera: P(6|C).

El condicionamiento de probabilidades puede lograrse aplicando el teorema de Bayes.

Dado un espacio de probabilidad ${\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )}$ y dos eventos (o sucesos) ${\displaystyle A,B\in {\mathcal {F}}}$ con ${\displaystyle P(B)>0}$, la probabilidad condicional de A dado B está definida como:

Como ya vimos en la probabilidad condicional, la probabilidad de un evento puede ser afectada por la ocurrencia de otro, cuando esto sucede se dice que los eventos son dependientes. Y por el contrario si la ocurrencia de uno de ellos no afecta al otro se dice que son eventos independientes.

En el ejemplo 1 de la condicional tenemos que los eventos sangre O y factor Rh- son dependientes, ya que la condición del factor Rh afecta la probabilidad de que la persona elegida tenga sangre tipo O.

De hecho en el ejemplo 3 de la condicional los eventos caiga sol y caiga 5 son independientes, el hecho de que en la moneda caiga sol no afecta en nada al dado, y la probabilidad de que caiga un 5 es la misma que si tiramos únicamente el dado( igual a 1/ 6).

Una forma de distinguir si dos eventos A y B son independientes es si se cumple que:

P (B | A)  = P(B)     o si     P (A | B)  = P(A)   (De otro modo los eventos son dependientes).

La ley de la multiplicación es útil para calcular la probabilidad de que ocurran los eventos A y B de forma conjunta, esta ley se basa en la definición de probabilidad condicional despejando P(A y B) tenemos:

Ejemplo 1. En un centro comercial el cajero por experiencia sabe que 60% de los clientes usan tarjeta de crédito para pagar sus compras

a) ¿Cuál es la probabilidad de que los dos siguientes clientes paguen con tarjeta de crédito?

Sean los eventos
A = el primer cliente paga con tarjeta de crédito
B = el segundo cliente paga con tarjeta de crédito

Podemos suponer que A y B son independientes, ya que si un cliente usa la tarjeta no debe afectar que otro cliente la use. Por tanto la probabilidad buscada es

P(A y B) = P(A) P(B) = (0.60) (0.60) = 0.36

b) ¿Cuál es la probabilidad de que los dos siguientes clientes no paguen con tarjeta de crédito?

Sean los eventos
C = el primer cliente no paga con tarjeta de crédito
D = el segundo cliente no paga con tarjeta de crédito

Nuevamente podemos suponer que A y B son independientes, y que P(C) = P(D) = 0.40

Por tanto la probabilidad buscada es P(C y D) = P(C) P(D) = (0.40) (0.40) = 0.16

c) ¿Cuál es la probabilidad de que uno de los dos siguientes clientes no paguen con tarjeta de crédito?

Este evento nos pide que solo uno pague con tarjeta pero no dice en qué orden, así que tenemos dos posibilidades:
- El primero paga con tarjeta y el segundo no paga con tarjeta (A y D)
- El primero no paga con tarjeta y el segundo paga con tarjeta (C y B)

Entonces la probabilidad buscada la podemos escribir como P (alguno pague con tarjeta) =

P(A y D) + P(C y B) = P(A) P(D) +  P(C) P(B) = (0.60) (0.40) + (0.40) (0.60) = 0.24 + 0.24 = 0.48

(Estos tres resultados forman el espacio muestral, podemos comprobarlo si sumamos las tres probabilidades, obteniendo 0.36 + 0.16 + 0.48 = 1)

INDEPENDENCIA ESTADISTICA

En teoría de probabilidades, se dice que dos sucesos aleatorios son independientes entre sí cuando la probabilidad de cada uno de ellos no está influida porque el otro suceso ocurra o no, es decir, cuando ambos sucesos no están relacionados.

Dos sucesos son independientes si la probabilidad de que ocurran ambos simultáneamente es igual al producto de las probabilidades de que ocurra cada uno de ellos, es decir, si ${\displaystyle P(A\cap B)=P(A)P(B)}$

Motivación de la definición

Sean ${\displaystyle A}$ y ${\displaystyle B}$ dos sucesos tales que ${\displaystyle P(B)>0}$, intuitivamente A es independiente de B si la probabilidad de A condicionada por B es igual a la probabilidad de A. Es decir si:

${\displaystyle P(A|B)=P(A)\,}$

De la propia definición de probabilidad condicionada:

${\displaystyle P(A|B)={\frac {P(A\cap B)}{P(B)}}}$

se deduce que ${\displaystyle P(A\cap B)=\ P(A|B)P(B),}$ y dado que ${\displaystyle P(A|B)\ =\ P(A)}$ deducimos trivialmente que ${\displaystyle P(A\cap B)=P(A)P(B)\,}$.

Si el suceso A es independiente del suceso B, automáticamente el suceso B es independiente de A.

Teorema de Bayes

El teorema de Bayes es utilizado para calcular la probabilidad de un suceso, teniendo información de antemano sobre ese suceso.

Podemos calcular la probabilidad de un suceso A, sabiendo además que ese A cumple cierta característica que condiciona su probabilidad.  El teorema de Bayes entiende la probabilidad de forma inversa al teorema de la probabilidad total. El teorema de la probabilidad total hace inferencia sobre un suceso B, a partir de los resultados de los sucesos A. Por su parte, Bayes calcula la probabilidad de A condicionado a B.

El teorema de Bayes ha sido muy cuestionado. Lo cual se ha debido, principalmente, a su mala aplicación. Ya que, mientras se cumplan los supuestos de sucesos disjuntos y exhaustivos, el teorema es totalmente válido.

Fórmula del teorema de Bayes

Para calcular la probabilidad tal como la definió Bayes en este tipo de sucesos, necesitamos una fórmula. La fórmula se define matemáticamente como:

Donde B es el suceso sobre el que tenemos información previa y A(n) son los distintos sucesos condicionados. En la parte del numerador tenemos la probabilidad condicionada, y en la parte de abajo la probabilidad total. En cualquier caso, aunque la fórmula parezca un poco abstracta, es muy sencilla. Para demostrarlo, utilizaremos un ejemplo en el que en lugar de A(1), A(2) y A(3), utilizaremos directamente A, B y C.

Ejemplo del teorema de Bayes

Una empresa tiene una fábrica en Estados Unidos que dispone de tres máquinas A, B y C, que producen envases para botellas de agua. Se sabe que la máquina A produce un 40% de la cantidad total, la máquina B un 30% , y la máquina C un 20%. También se sabe que cada máquina produce envases defectuosos. De tal manera que la máquina A produce un 2% de envases defectuosos sobre el total de su producción, la máquina B un 3%, y la máquina C un 5%. Dicho esto, se plantean dos cuestiones:

P(A) = 0,40      P(D/A) = 0,02

P(B) = 0,30      P(D/B) = 0,03

P(C) = 0,30      P(D/C) = 0,05

1.Si un envase ha sido fabricado por la fábrica de esta empresa en Estados Unidos ¿Cuál es la probabilidad de que sea defectuoso?

Se calcula la probabilidad total. Ya que, a partir los diferentes sucesos, calculamos la probabilidad de que sea defectuoso.

PERMUTACIÓNES SIN REPETICIÓN DE n ELEMENTOS TOMADOS TODOS A LA VEZ

Ejemplo 4: 

¿De cuántas formas diferentes se pueden ordenar las letras de la palabra IMPUREZA?

Solución: Puesto que tenemos 8 letras diferentes y las vamos a ordenar en diferentes formas, tendremos 8 posibilidades de escoger la primera letra para nuestro arreglo, una vez usada una, nos quedan 7 posibilidades de escoger una segunda letra, y una vez que hayamos usado dos, nos quedan 6, así sucesivamente hasta agotarlas, en total tenemos:

8 ´ 7 ´ 6 ´ 5 ´ 4 ´ 3 ´ 2 ´ 1 = 40320

PERMUTACIÓNES CIRCULARES

Ahora estudiaremos algunos ejemplos de arreglos circulares, sabemos que si queremos sentar a cuatro personas una al lado de la otra en fila, el número de arreglos que podemos hacer es 4!; ahora bien, si las queremos sentar alrededor de una mesa circular, ¿de cuántas formas lo podemos hacer?

Observemos los siguientes arreglos:

Por cada una de las permutaciones o arreglos circulares tenemos 4 de ellos diferentes en fila; esto es, el arreglo circular 1 puede leerse en sentido contrario a las agujas del reloj de las siguientes formas: ABCD, BCDA, CDAB, y DABC, que son 4 arreglos diferentes si fueran en filas; pero es un solo arreglo circular. Entonces, en lugar de tener 4! que es el número de arreglos en fila.

TENEMOS SOLAMENTE: